Gracias al Internet y a las telecomunicaciones, hoy día tenemos acceso a montañas de información. Sin embargo, no toda es verdadera, y las matemáticas no se salvan de ello.
Muchas personas, cuando estudian matemáticas en la escuela o el colegio, le preguntan a los profesores qué importancia tienen. Quizá a esto se deba que mucha gente trate de relacionar conceptos matemáticos con la vida diaria, o que cuente historias interesantes relacionadas a la matemática, como una manera de buscar el interés de los y las estudiantes. Sin embargo, al igual que en otras áreas, a veces nos encontramos con bulos o información falsa, que lejos de ayudarnos podría ser más bien perjudicial. A continuación te presentamos tres mitos relacionados con la matemática que son falsos.
La espiral de Fibonacci está en todas partes
Uno de los mitos matemáticos más populares es el de la espiral de Fibonacci. Por si no la conocés, la espiral de Fibonacci (también conocida como la espiral áurea) es una espiral que cumple con la siguiente propiedad: si dibujás dos cuadrados de lado 1 uno junto al otro, luego otro de lado 2 junto a ellos, luego otro de lado 3, otro de lado 5, otro de lado 8, y así sucesivamente, siguiendo los números de la famosa sucesión de Fibonacci, se forma la espiral con algunos de los vértices de los cuadrados. Es más sencillo verla en una imagen:
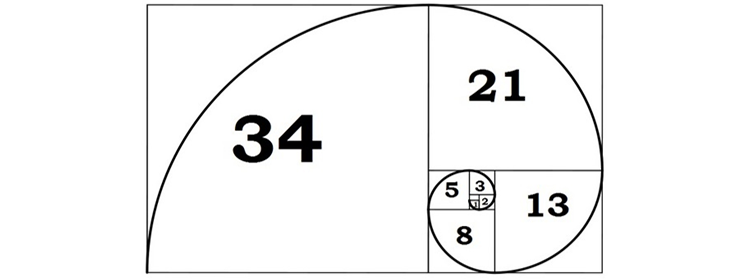
Según el mito, esta espiral se encuentra en muchos sitios en la naturaleza; por ejemplo, en las conchas, la cola del camaleón o ciertas plantas. Quizá alguna vez hayás visto una imagen como esta:
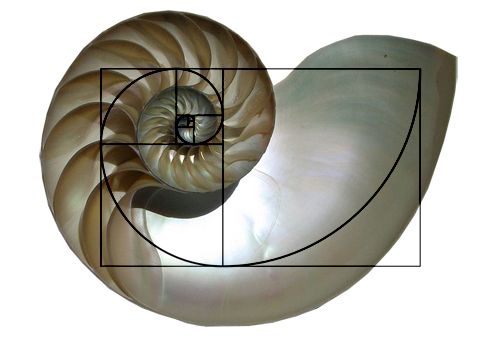
Además, se dice que los humanos solemos encontrar esta espiral muy estética, y es la razón por la que se incluya en muchos trabajos, desde el Partenón:

Hasta el logo de Apple:

Lo cierto es que la espiral de Fibonacci no es más común en la naturaleza que otras espirales. Muchas veces, se modifica las imágenes en las que se superpone la espiral a un elemento natural modificando la longitud de los lados de los cuadrados o torciendo la espiral de alguna manera para que calce con la fotografía. Incluso, si te fijás bien en la imagen del caracol que hemos incluido más arriba, podrás darte cuenta de que la espiral de Fibonacci «se cierra» más rápidamente que la de la concha en la fotografía; no son la misma espiral. Algunos estudios hechos por Keith Devlin, investigador de la Universidad de Stanford y comunicador de la matemática, demuestran también que los humanos no encontramos las figuras relacionadas con la sucesión de Fibonacci más placenteras a la vista que otras.
Pi contiene toda la información de tu vida

Hace tiempo rondan en redes sociales imágenes como la anterior, en las que se afirma que, dado que la expansión decimal de pi es infinita y sus dígitos no se repiten de manera periódica, esto implica que contiene cualquier posible cadena de caracteres, por lo que en alguna parte de pi podrías encontrar desde tu nombre hasta una película entera de tu vida. El problema con esta imagen es que el razonamiento es inválido; que el número sea infinito y que sus dígitos no se repitan periódicamente no implica que contenga cualquier posible cadena de caracteres. Por ejemplo, el siguiente número cumple con la misma premisa:
0,10100100010000100000100000010000000100000000…
Este número tiene una cantidad infinita de dígitos que no se repiten de manera periódica; sin embargo, en ninguna parte de este número aparece, por ejemplo, la cadena de dígitos 7586484. Alguna gente podría argumentar que esto no importa, puesto que podemos interpretar los datos en binario (usando solo ceros y unos), pero aun si lo hiciéramos así, sería imposible encontrar en este número la cadena 01111010, la cual codifica en ASCII la letra ‘z’. Así que si el nombre de tu verdadero amor se escribe con ‘z’ no lo vas a encontrar aquí.
De la misma manera, este razonamiento es inválido para el número pi. A los números que sí tienen esta propiedad se les conoce con el nombre de «números normales» . El problema con pi es que no se ha demostrado si es o no un número normal (aunque se sospecha que sí lo es). Si querés ver un número que sí es normal, y que por lo tanto sí contiene todo lo que dice la imagen, podés tomar este:
0,0123456789101112131415161718192021222324252627…
Gauss encontró la fórmula para sumar los primeros n números cuando estaba en la escuela
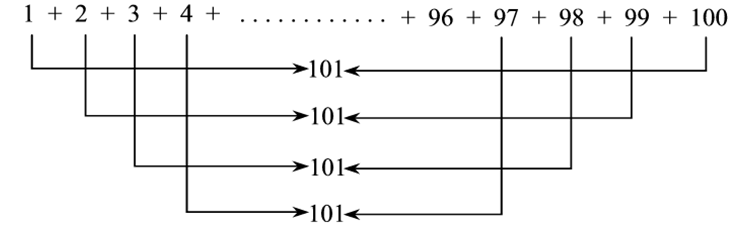
Si alguna vez has asistido a una clase de matemáticas, es muy probable que hayás escuchado esta historia. Si no, te contamos una de sus múltiples versiones: de acuerdo con el relato, el famoso matemático Carl Friedrich Gauss era muy inquieto de niño. Un día, para que se calmara un rato, la maestra de la escuela le asignó como tarea sumar todos los números naturales del uno al cien; ella esperaba que esto le tomara mucho tiempo. Al cabo de solo un par de minutos, Gauss había dado con la respuesta correcta. La maestra no pudo explicarse cómo había llegado un niño a esa respuesta tan rápidamente, por lo que Gauss a continuación le explica cómo encontró una fórmula que le permite conocer rápidamente, el resultado de sumar los primeros números naturales.
Es en esta parte del relato, donde el profesor suele explicar cómo se obtiene la fórmula. El razonamiento es sencillo, lo cual suele hacer más creíble para los estudiantes universitarios que un niño de escuela haya podido encontrar la fórmula, y más aun si ese niño era alguien tan inteligente como Gauss.
Sin embargo, la historia es apócrifa. No se sabe muy bien quién la inventó, aunque suele atribuirse su origen a un libro escrito por Wolfgang Sartorius, en el cual relata una anécdota que Gauss le contara en vida, en la cual este último logró resolver muy rápidamente un problema matemático el primer día de escuela. El libro no menciona cuál fue ese problema exactamente. Lo que sí se sabe a ciencia cierta es que la fórmula ya era conocida, por lo menos, desde el siglo VIII, diez siglos antes del nacimiento de Gauss.
Todo esto nos sirve para recordar que hay mucha información falsa rondando por ahí, no solo en Internet, sino también de boca en boca. Y mientras que en las matemáticas puede ser relativamente inofensiva, en otros campos esta clase de información puede ser dañina. Recordemos siempre verificar la certeza de lo que compartimos con otros, ya sea a través de una pantalla o cara a cara.