Cómo un problema tan simple como colorear un mapa está cambiado por completo la perspectiva moderna de la matemática.
En la disciplina matemática, los problemas más interesantes suelen ser aquellos que, a pesar de tener un planteamiento sencillo de entender, tienen una solución que requiere de un entendimiento profundo. Muchas veces, la resolución de un problema de este tipo lleva a la creación de una nueva rama de la matemática, con la cual se puede resolver toda una clase de problemas no resueltos anteriormente. Es en este contexto donde se ubica el, quizá infame, Teorema de los Cuatro Colores.
La Conjetura de los Cuatro Colores fue planteada por primera vez en 1852 por Francis Guthrie, botánico y matemático, después de haber estado coloreando un mapa de Inglaterra. Guthrie observó que era posible colorear cualquier mapa que se le ocurriera usando tan solo 4 colores, de tal manera que dos regiones que limitaran una con la otra no tuviesen el mismo color.
Intentó probar esto matemáticamente. Al no poder lograrlo, le comentó el problema a su hermano, Frederick, quien era físico y químico. Frederik a su vez le relató el problema a Augustus De Morgan, quien era profesor de matemáticas suyo en ese momento. De Morgan tampoco pudo probarlo y le envió una carta a William Rowan Hamilton en la que le explicaba el problema. A partir de aquí es cuando la conjetura comienza a ganar popularidad (Blanda, 2014).

Francis Guthrie
En 1879, Alfred Kempe publicó un artículo en el que aseguraba haber demostrado el teorema, haciendo uso de una nueva teoría inventada por él mismo, que más tarde pasaría a conocerse por el nombre de «Cadenas de Kempe». En 1880, Peter Guthrie Tait, independientemente de Kempe, desarrolló otra supuesta prueba del teorema (Blanda, 2014). Ambas resultaron ser erróneas, aunque el error en la prueba de Kempe no fue descubierto sino hasta 11 años después (Calude, 2001).

Alfred Kempe
Varias pruebas, todas erróneas, siguieron a estas dos hasta 1976, cuando Kenneth Appel y Wolfgang Haken publicaron un resultado que al día de hoy sigue siendo controversial. Appel y Haken lograron demostrar que el Problema de los Cuatro Colores podía ser reducido a un número finito de mapas. Si lograban demostrar que para todos estos mapas bastaban 4 colores, el teorema sería cierto en general.
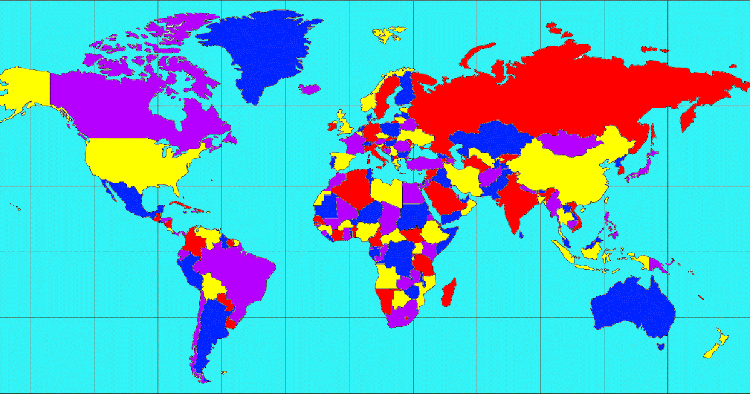
Mapa del mundo coloreado con solo 4 colores.
La parte controversial de la solución no es esa, sino la siguiente: el número de casos a los que Appel y Haken redujeron el problema era de casi 2000. Era una cantidad demasiado grande como para que un humano pudiera revisar todos estos casos a mano (el trabajo necesario para revisar un solo caso ya es bastante grande) (Rogers, 2008).
Por tanto, los investigadores decidieron hacer uso de computadoras para verificar que el teorema se cumplía en estos (casi) 2000 casos. Los algoritmos que usaron, hoy en día, podrían ser ejecutados por cualquier PC. Sin embargo, en su momento, Appel y Haken debieron hacer uso de más de 1200 horas de computación, corriendo el programa varias veces en distintas computadoras para asegurarse del resultado. Esta fue la primera prueba matemática asistida por computadora en la historia (Rjlipton, 2009).
La comunidad matemática no recibió muy bien este resultado. Muchos argumentaron que esta prueba se reducía a «es cierto porque la computadora lo dijo«, lo cual sería equivalente a decir «es cierto porque von Neumann dijo: ¿cómo sabemos que no se equivocó? (Bailey & Borwein, 2013) Otros argumentaron que la correctitud de la prueba no era verificable, puesto que incluso solo chequear 2000 casos no era tarea fácil.
Un tercer argumento presentado en contra de esta prueba fue que no proveía ningún entendimiento nuevo. Es decir, que no nos da ninguna información de por qué este número es 4 y no 5, o 6, o 13 (Calude, 2001).
Con el tiempo, sin embargo, la prueba ha ido ganando aceptación. El argumento de no poder estar seguros de que la computadora no se haya equivocado se ha rechazado por ser inválido: un humano también puede equivocarse, como la misma prueba de Kempe lo evidencia. Además, la probabilidad de que una máquina se equivoque en un proceso de mero cómputo es mucho menor que la de que un humano lo haga.
También se ha argumentado que una computadora es simplemente una herramienta moderna que podemos usar para asistir las pruebas: ¿para qué ir a pie al trabajo si se puede ir en carro? (Calude, 2001)

Mapa inexistente coloreado con solo 4 colores.
Algunos matemáticos han logrado también reducir un poco más el número de casos necesarios para verificar el teorema. Actualmente, la mejor solución que se ha hallado considera alrededor de 600 casos (Rogers, 2008).
La prueba de Appel y Haken sí nos ha provisto de un nuevo entendimiento, puesto que ha llevado a los matemáticos a cuestionarse filosóficamente la naturaleza de una prueba: ¿Cuándo es una prueba válida? ¿Realmente es una demostración matemática tan objetiva y absolutamente verdadera como se pensaba?
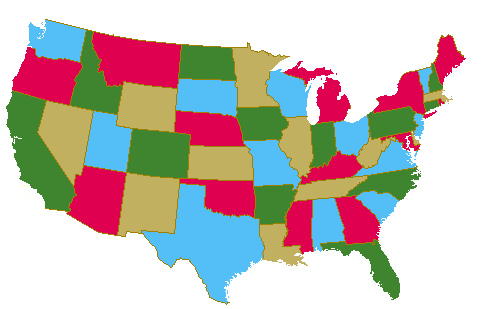
Mapa de los condados de EE.UU. con solo 4 colores.
Posteriormente a esta, han habido otras demostraciones asistidas por computadoras, como la prueba del Teorema de Kepler (esta también tiene un planteamiento sencillo. La forma más eficiente de «acomodar» esferas en el espacio es exactamente como apilan las naranjas en el supermercado (Wikipedia, 2017)).
Gracias a este tipo de pruebas, está surgiendo un nuevo tipo de matemática, llamada matemática experimental, en la cual se hace uso de herramientas computacionales para observar patrones y buscar propiedades comunes de objetos abstractos (Bailey & Borwein, 2013; Wolfram, 2017; Wikipedia, 2017).

Imagen ilustrativa del Teorema de Kepler.
El paradigma que se ha manejado hasta el momento, en el que se ve a la matemática como una disciplina puramente deductiva, está comenzando a ser desplazado por un nuevo paradigma. En este se aceptan los procesos de prueba y error, experimentación y formulación de conjeturas como una parte esencial del quehacer matemático.
Relacionado a esto, se ha señalado que el concepto de una prueba o demostración matemática es un constructo social, y como tal, no siempre ha existido (Calude, 2001). Al inicio de la Edad Antigua, por ejemplo, muchos teoremas matemáticos se «demostraban» simplemente verificando que se cumplían para muchos casos (e.g. las tablas aritméticas de Babilonia (Wikipedia, 2017)).
En todo caso, la ganancia que nos ha proporcionado este teorema, con un planteamiento tan simple que hasta un niño puede entenderlo, ha sido grande. Aun después de la resolución del problema, seguimos aprendiendo de él, generando nuevo conocimiento, entendiendo mejor el mundo que nos rodea.
Bibliografía
Bailey, D. H., & Borwein, J. M. (8 de julio de 2013). The Colorful Life of the Four-color Theorem: A tribute to Kenneth Appel. Recuperado el 17 de mayo de 2017, de http://www.huffingtonpost.com/david-h-bailey/kenneth-appel-four-color-theorem_b_3233775.html
Blanda, S. (29 de junio de 2014). The Four Color Theorem: AMS Blogs. Recuperado el 17 de mayo de 2017, de http://blogs.ams.org/mathgradblog/2014/06/29/color-theorem/
Calude, A. S. (2001). The Journey of the Four Colour Theorem Through Time. The New Zealand Mathematics Magazine , 27-35.
rjlipton. (24 de abril de 2009). The Four Color Theorem: Gödel’s Lost Letter and P=NP. Recuperado el 17 de mayo de 2017, de https://rjlipton.wordpress.com/2009/04/24/the-four-color-theorem/
Rogers, L. (setiembre de 2008). The Four Colour Theorem: NRICH. Recuperado el 17 de mayo de 2017, de http://nrich.maths.org/6291
Wikipedia. (6 de febrero de 2017). Babylonian mathematics: Wikipedia. Recuperado el 17 de mayo de 2017, de https://en.wikipedia.org/wiki/Babylonian_mathematics
Wikipedia. (3 de mayo de 2017). Experimental Mathematics: Wikipedia. Recuperado el 17 de mayo de 2017, de https://en.wikipedia.org/wiki/Experimental_mathematics
Wikipedia. (24 de abril de 2017). Kepler conjecture: Wikipedia. Recuperado el 17 de mayo de 2017, de https://en.wikipedia.org/wiki/Kepler_conjecture
Wolfram, S. (6 de marzo de 2017). Two Hours of Experimental Mathematics: Stephen Wolfran Blog. Recuperado el 17 de mayo de 2017, de http://blog.stephenwolfram.com/2017/03/two-hours-of-experimental-mathematics/