Hace 157 años se propuso un problema matemático cuya solución no conocemos. ¿Qué ventajas supondría su resolución para la matemática contemporánea?
En 1859, el famoso matemático alemán Bernhard Riemann formuló un problema que al día de hoy aún no ha podido ser resuelto. Riemann demostró además que este problema tiene relación con la distribución de los números primos. Esto, a su vez, cobra gran importancia hoy día en el campo de la informática, especialmente en el de la criptografía. Si se demuestra que la Hipótesis de Riemann es correcta, esto implicaría que los números primos tienen una estructura más o menos definida, lo cual facilitaría el encontrarlos, y sería necesario buscar nuevas técnicas de seguridad informática.
Para explicar en qué consiste este problema, debemos considerar primero la función zeta de Riemann:
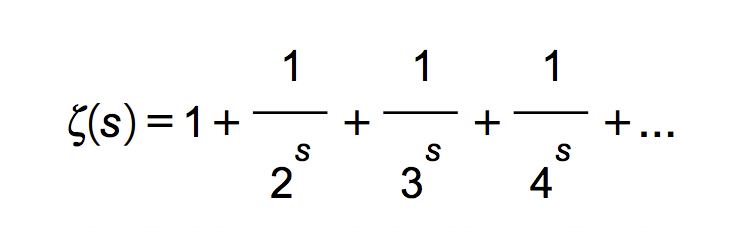
En términos simples, una función es un mecanismo que le asigna a un número otro valor. Por ejemplo, la función f(x)=x+1 le asigna a cada número el valor del mismo más uno; es decir, que al número 1 le asigna 2, al 23 le asigna 24, a 4,5 le asigna 5,5 y a π le asigna π+1.
La función zeta de Riemann, contiene en su fórmula una «suma infinita» (también llamada «serie» en matemáticas). Por supuesto, los humanos y las computadoras podemos sumar una cantidad finita de números, pero ¿qué significa «sumar una cantidad infinita de números»? Existen formas en las que se le puede dar sentido a algunas de estas sumas; sin embargo, no es posible hacerlo para todas las series. En el caso en que estas sumas tengan algún sentido, se dice que la serie es «convergente», y en el caso en el que no, se dice que es «divergente».
Para la función zeta, esta serie converge solo cuando s es mayor que 1. Para otros valores, esta suma simplemente no tiene sentido. Por ejemplo, si tomamos s=-1, vemos que la función se convierte en ζ(-1)=1+2+3+4+⋯. No podemos asignarle un número concreto a esta serie, ya que es claro que, al ir sumando, vamos alcanzando valores cada vez mayores.
Los números complejos
Para llegar al problema planteado por Riemann, ahora debemos tomar otro desvío: los números complejos.
(Con ese nombre es normal que no los veamos en bachi).
Muchos conocemos del colegio los números reales. Se ha mostrado ya muchas veces que los números reales pueden ser representados por medio de una recta, donde cada punto corresponde a un número real y cada número real tiene un punto en la recta que le corresponde. Sin embargo, hay una expresión que ha intrigado a los matemáticos desde hace mucho tiempo: la raíz cuadrada de menos uno.
Al estudiar esta expresión, los matemáticos descubrieron que la raíz cuadrada de menos uno no forma parte de los números reales. Sin embargo, sabiendo que ya antes se había ampliado el sistema numérico utilizado, se decidió simplemente ampliar el sistema una vez más para incluir este número, al cual llamaron i. No obstante, debido a que i no puede ser colocado en la recta real, se decidió colocarlo en una nueva recta, perpendicular a la anterior. Esto generó lo que hoy conocemos como el «plano complejo». La colección de todos los números que se encuentran representados en este plano es conocida por el nombre de «los números complejos».
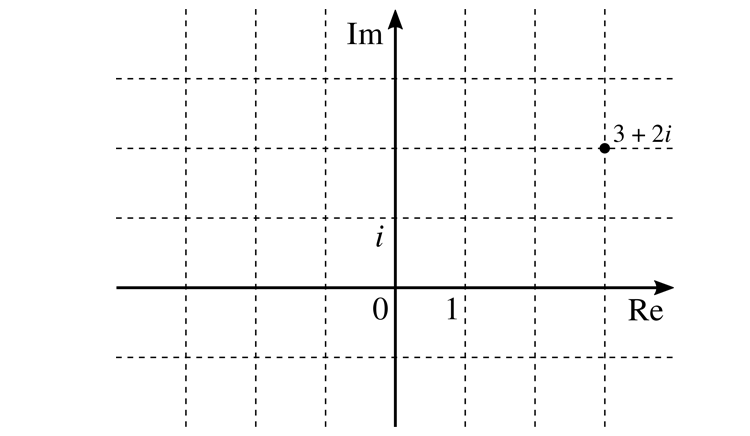
(Se ve un poco simple para ser el plano complejo).
Con esta herramienta, podemos continuar explicando el razonamiento de Riemann. El famoso matemático descubrió que, al extender su función para que funcionara en los números complejos en vez de funcionar solamente en los reales, esta mostraba valores convergentes para todos aquellos números complejos a la derecha de la recta vertical que pasa por 1 en el plano complejo. Esto a su vez le permitió, con ayuda de teoremas ya conocidos, extender la función, de manera que esta también obtuviese números válidos en el resto del plano complejo (https://www.britannica.com/topic/Riemann-zeta-function). De esta manera, Riemann obtuvo resultados tan sorprendentes como el siguiente:
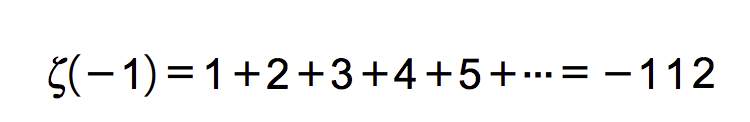
El problema
Ahora bien, ¿cuál es la pregunta que Riemann no pudo contestar? Su formulación es muy simple: ¿para qué valores complejos de s ocurre que ζ(s)=0? Existen algunos valores muy fáciles de encontrar, llamados «triviales»; sin embargo, se sabe que no son todos. Riemann conjeturó que todos los valores no triviales donde la función zeta se hace cero se encuentran sobre la recta vertical que pasa por 1/2 en el plano complejo. No obstante, hasta el día de hoy nadie ha podido demostrar que esto sea cierto. Y tampoco se ha podido refutar.
La solución a este problema no solo nos permitiría encontrar estructuras desconocidas en los tan interesantes números primos, sino que también tiene aplicaciones prácticas, con muchos interesados en la solución de este problema. Incluso aunque la hipótesis resulte ser incorrecta, es muy posible que el trabajo que se requiera para resolver este problema nos abra las puertas a una nueva rama de las matemáticas, con aplicaciones aún desconocidas. La solución de este problema nos podría ayudar a comprender mejor el universo.
Nota: La imagen de la recta numérica de los números complejos y la del plano complejo son de Wikimedia Commons.